算法练习专栏——Codeforces——Codeforces Round 937 (Div. 4)

D. Product of Binary Decimals

Let’s call a number a binary decimal if it is a positive integer and all digits in its decimal notation are either $0$ or $1$. For example, $1,010,111$ is a binary decimal, while $10,201$ and $787,788$ are not.

Given a number $n$, you are asked whether or not it is possible to represent $n$ as a product of some (not necessarily distinct) binary decimals.

Input

The first line contains a single integer $t$ ($1 \leq t \leq 5 \cdot 10^4$) — the number of test cases.

The only line of each test case contains a single integer $n$ ($1 \leq n \leq 10^5$).

Output

For each test case, output “YES” (without quotes) if $n$ can be represented as a product of binary decimals, and “NO” (without quotes) otherwise.

You can output “YES” and “NO” in any case (for example, strings “yES”, “yes”, and “Yes” will be recognized as a positive response).

Example

input

output

YES
YES
YES
YES
YES
YES
NO
NO
NO
NO
YES

Note

The first five test cases can be represented as a product of binary decimals as follows:

$121 = 11 \times 11$.
$1 = 1$ is already a binary decimal.
$14,641 = 11 \times 11 \times 11 \times 11$.
$12,221 = 11 \times 11 \times 101$.
$10,110 = 10,110$ is already a binary decimal.

翻译

如果一个数字是正整数，并且其十进制表示法中的所有数字都是 $0$ 或 $1$ ，那么我们将其称为二进制小数。例如， $1,010,111$ 是二进制十进制，而 $10,201$ 和 $787,788$ 则不是。

给定一个数字 $n$ ，系统会询问您是否可以将 $n$ 表示为一些（不一定不同）二进制小数的乘积。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 5 \cdot 10^4$ ) - 测试用例的数量。

每个测试用例的唯一行包含一个整数 $n$ ( $1 \leq n \leq 10^5$ )。

输出

对于每个测试用例，如果 $n$ 可以表示为二进制小数的乘积，则输出“YES”（不带引号），否则输出“NO”（不带引号）。

您可以在任何情况下输出“YES”和“NO”（例如，字符串“yES”、“yes”和“Yes”将被识别为肯定响应）。

Example

input

output

YES
YES
YES
YES
YES
YES
NO
NO
NO
NO
YES

思路

就是将所有由1和0组成的数除尽为止,看看是否可以除到1.一个小小的DFS

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
// #define max(a, b) ((a) > (b) ? (a) : (b))
// #define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 510, M = 5e3 + 10;
int a[N], b[N], c[N];
LL ans = INF;
int n, k;

void gio(int i){
    if(i>n)return;
    gio(i*10); gio(i*10+1);
    if(i!=1)
        while(n%i==0)n/=i;
}

void solve() {
    cin >> n;
    gio(1);
    if(n == 1) cout << "YES\n";
    else cout << "NO\n";
}


int main()
{
    
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    return 0;
}

E. Nearly Shortest Repeating Substring

原题

You are given a string $s$ of length $n$ consisting of lowercase Latin characters. Find the length of the shortest string $k$ such that several (possibly one) copies of $k$ can be concatenated together to form a string with the same length as $s$ and, at most, one different character.

More formally, find the length of the shortest string $k$ such that $c = \underbrace{k + \cdots + k}_{x\rm\ \text{times}}$ for some positive integer $x$, strings $s$ and $c$ has the same length and $c_i \neq s_i$ for at most one $i$ (i.e. there exist $0$ or $1$ such positions).

Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^3$) — the number of test cases.

The first line of each test case contains a single integer $n$ ($1 \leq n \leq 2\cdot10^5$) — the length of string $s$.

The second line of each test case contains the string $s$, consisting of lowercase Latin characters.

The sum of $n$ over all test cases does not exceed $2\cdot10^5$.

Output

For each test case, print the length of the shortest string $k$ satisfying the constraints in the statement.

Example

input

5
4
abaa
4
abba
13
slavicgslavic
8
hshahaha
20
stormflamestornflame

output

Note

In the first test case, you can select $k = \texttt{a}$ and $k+k+k+k = \texttt{aaaa}$, which only differs from $s$ in the second position.

In the second test case, you cannot select $k$ of length one or two. We can have $k = \texttt{abba}$, which is equal to $s$.

翻译

给您一个长度为 $n$ 的字符串 $s$ ，由小写拉丁字符组成。求最短字符串 $k$ 的长度，以便可以将多个(可能是一个) $k$ 的副本连接在一起，形成一个与 $s$ 长度相同且最多有一个不同字符的字符串。

更正式地说，找到最短字符串 $k$ 的长度，使得对于某个正整数 $x$ ，字符串 $c = \underbrace{k + \cdots + k} _ {x\rm\ \text{times}}$ 、字符串 $s$ 和 $c$ 具有相同的长度，对于最多一个 $i$ ，字符串 $c _ i \neq s _ i$ (即存在 $0$ 或 $1$ 这样的位置）。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 10^3$ ) - 测试用例的数量。

每个测试用例的第一行包含一个整数 $n$ ( $1 \leq n \leq 2\cdot10^5$ ) - 字符串 $s$ 的长度。

每个测试用例的第二行包含字符串 $s$ ，由小写拉丁字符组成。

所有测试用例的 $n$ 之和不超过 $2\cdot10^5$ 。

输出

对于每个测试用例，打印满足语句中约束的最短字符串 $k$ 的长度。

Example

input

5
4
abaa
4
abba
13
slavicgslavic
8
hshahaha
20
stormflamestornflame

output

思路

这里我们可以这样思考.首先,我们要想实现组合为一个和s一样长度的字符串,这个子字符串长度一定得是n的因数对不对.其二需要考虑的就是我们以每x个字符为一组,那么我们看看s的没x个字符为一组的字符串中的差距就好了,如果差距只有1或者0,那么我们就输出len即可,反之则需要增加len查询.举个例子:hshahaha 这个字符串,首先我们按照每1个字符为一组看看,就分为了h,s,h,a,h,a,h,a,这些组合的差异可想而知,是非常大的,所以这组肯定是不可以的.下面就是每2个字符为一组看看,就分为了hs,ha,ha,ha这么几组,我们可以发发现这个差距只有1对不对,这一组就直接正确,后面len更大的情况也不用再查看了,输出当前的len=2即可,反之差距还是很大,我们还是需要往后面继续判断,最后最大我们就是输出n本身.

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
// #define max(a, b) ((a) > (b) ? (a) : (b))
// #define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
const int N = 510, M = 5e3 + 10;
int a[N], b[N], c[N];
LL ans = INF;
int n, k;

void solve() {
    int n;
    cin >> n;
    string s;
    cin >> s;
    for (int len = 1; len <= n; len++) {
        if (n % len == 0) {
            int sum = 0;
            for (int r = 0; r < len; r++) {
                vector<int> cnt(26, 0);
                int mx = 0;
                for (int i = r; i < n; i += len) {
                    int c = int(s[i] - 'a');
                    cnt[c] += 1;
                    mx = max(mx, cnt[c]);
                }
                sum += mx;
            }
            if (sum >= n - 1) {
                cout << len << ed;
                break;
            }
        }
    }
}


int main()
{
    
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    return 0;
}

F. 0, 1, 2, Tree!

原题

Find the minimum height of a rooted tree$^{\dagger}$ with $a+b+c$ vertices that satisfies the following conditions:

$a$ vertices have exactly $2$ children,
$b$ vertices have exactly $1$ child, and
$c$ vertices have exactly $0$ children.

If no such tree exists, you should report it.

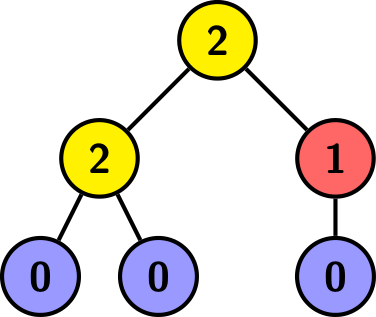
The tree above is rooted at the top vertex, and each vertex is labeled with the number of children it has. Here $a=2$, $b=1$, $c=3$, and the height is $2$.

$^{\dagger}$ A rooted tree is a connected graph without cycles, with a special vertex called the root. In a rooted tree, among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child.

The distance between two vertices in a tree is the number of edges in the shortest path between them. The height of a rooted tree is the maximum distance from a vertex to the root.

Input

The first line contains an integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The only line of each test case contains three integers $a$, $b$, and $c$ ($0 \leq a, b, c \leq 10^5$; $1 \leq a + b + c$).

The sum of $a + b + c$ over all test cases does not exceed $3 \cdot 10^5$.

Output

For each test case, if no such tree exists, output $-1$. Otherwise, output one integer — the minimum height of a tree satisfying the conditions in the statement.

Example

input

Copy

output

Copy

Note

The first test case is pictured in the statement. It can be proven that you can’t get a height smaller than $2$.

In the second test case, you can form a tree with a single vertex and no edges. It has height $0$, which is clearly optimal.

In the third test case, you can form a tree with two vertices joined by a single edge. It has height $1$, which is clearly optimal.

翻译

求满足以下条件的具有 $a+b+c$ 顶点的有根树 $^{\dagger}$ 的最小高度：

$a$ 顶点恰好有 $2$ 个子节点，
$b$ 顶点恰好有 $1$ 子节点，并且
$c$ 顶点恰好有 $0$ 个子节点。

如果不存在这样的树，您应该报告它。

上面的树以顶部顶点为根，每个顶点都标有其子节点的数量。这里是 $a=2$ 、 $b=1$ 、 $c=3$ ，高度是 $2$ 。

$^{\dagger}$ 有根树是没有循环的连通图，具有称为根的特殊顶点。在有根树中，由边连接的任意两个顶点中，一个顶点是父顶点(距离根较近的顶点)，另一个顶点是子顶点。

树中两个顶点之间的距离是它们之间的最短路径中的边数。有根树的高度是从顶点到根的最大距离。

输入

第一行包含一个整数 $t$ ( $1 \leq t \leq 10^4$ ) - 测试用例的数量。

每个测试用例的唯一行包含三个整数 $a$ 、 $b$ 和 $c$ ( $0 \leq a, b, c \leq 10^5$ ； $1 \leq a + b + c$ )。

所有测试用例的 $a + b + c$ 之和不超过 $3 \cdot 10^5$ 。

输出

对于每个测试用例，如果不存在这样的树，则输出 $-1$ 。否则，输出一个整数——满足语句中条件的树的最小高度。

思路

什么时候无解？小结论：完全二叉树的叶子结点数量为树上结点的数量加一。也就是说只有 a + 1 = c 的时候才有解。

因为题目要求树高尽可能低，所以在使用 a 类结点的时候会构造为完全二叉树，然后从 b 类结点抽出一部分补充这颗完全二叉树，使其变成满二叉树，最后，将剩下的 b 类结点均摊的安排到满二叉树的叶子处即可。c 类结点的作用就是让树高加一，不需要去处理。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <unordered_map>
#include <string>
#include <cmath>
#include <set>
#include <stack>
#include <vector>
#include <deque>
#include <bitset>
#include <cstdio>
#include <iomanip>

// #define int long long
#define ull unsigned long long
#define ed '\n'
#define fi first
#define se second
#define fore(i, l, r) for(int i = (int)(l); i <=(int)r; i++)
#define debug(x) cout << "#x = " << x << ed;
#define PI acos(-1)
#define E exp(1)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define me0(st) memset(st, 0, sizeof st)
#define me3f(st) memset(st, 0x3f, sizeof st)
#define pdf(x) printf("%lf", double(x))
#define pif(x) printf("%d ",  int(x))
#define scf(x) printf("%d",  int(x))
#define re return 0
// #define max(a, b) ((a) > (b) ? (a) : (b))
// #define min(a, b) ((a) < (b) ? (a) : (b))
#define out(x, k) cout << fixed << setprecision(k) << x << ed

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef double db;


const int INF = 1e9;
int n, k;

void solve() {
    int a, b, c;
    cin >> a >> b >> c;
    
    if (a + 1 != c) {
      cout << -1 << ed;
    } else {
        int ans = 0;
        // a类结点放完之后的高度
        if (a != 0) ans = log2(a) + 1;
        // a类结点放完最下面一层还没放满的一层可以放的结点数
        int gap = (1 << ans) - a - 1;
        
        // 放b类结点
        b = b > gap ? b - gap : 0;
        
        // 看一直放可以继续放多少层
        ans += (b + c - 1) / c;
        cout << ans << ed;
    }
}


int main()
{
    
    int _ = 1;
    cin >> _;
    
    while(_--) {
        solve();
    }
    
    return 0;
}

算法练习专栏——Codeforces——Codeforces Round 939 (Div. 2) 上一篇

杂题——勇士传说下一篇