算法学习专栏——递归（DFS）

前言

递归这一种算法类型应该属于所有算法中比较绕的一种算法，对于讲解的难度比较大，即使是最简单的递归写法都可能很难用一个示意图来表示出来。比如说下面这段代码，大家应该可以看得出来：

#include <iostream>
using namespace std;
int sum(int n) {
	if (n != 1) return n + sum(n - 1);
	return n;
}
int n;
int main()
{
	cin >> n;
	
	cout << sum(n);

	return 0;
}

上述代码大家应该可以大概在脑袋中描绘出这个递归流程，但是如果想通过画图讲解出来就有点繁琐，个人感觉不太好表示。因此本节我的讲解应该可能还是以直播为主，笔记为辅的模式。

一、排列数字（简单+）

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

输出样例：

思路

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
const int N = 10;
int a[N];
bool st[N];
int n;
void dfs(int x) {
    if (x > n) {
        for (int i = 1; i <= n; i++) cout << a[i] << " ";
        puts("");
    }  
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            st[i] = true;
            a[x] = i;
            dfs(x + 1);
            a[x] = 0;
            st[i] = false;
        }
    }
}
int main()
{
    cin >> n;    
    dfs(1);    
    return 0;
}

二、八皇后（简单+++）

n−−皇后问题是指将 n 个皇后放在 n×n× 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

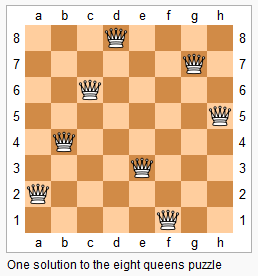
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

思路

代码

答案（请自己先思考一下再参考）

        
#include < iostream>
using namespace std;
const int N = 20;
char a[N][N];
bool cols[N],dg[N],udg[N];
int n;
void dfs(int x) {
    if (x > n) {
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++) {
                cout << a[i][j];    
            }
            puts("");
        }
        puts("");
    }  
    for (int i = 1; i <= n; i++) {
        if (!cols[i] && !dg[i + x] && !udg[n - x + i]) {
            a[x][i] = 'Q';
            cols[i] = dg[i + x] = udg[n - x + i] = true;
            dfs(x + 1);
            cols[i] = dg[i + x] = udg[n - x + i] = false;
            a[x][i] = '.';
        }
    }
}
int main()
{
    cin >> n;    
    for (int i = 1; i <= n; i++) 
    {
        for (int j = 1; j <= n; j++) {
            a[i][j] = '.';    
        }
    }
    dfs(1);    
    return 0;
}

算法学习专栏——深度优先遍历+BFS 上一篇

算法学习专栏——一、二维差分下一篇