算法练习专栏——队列+单调队列

前言

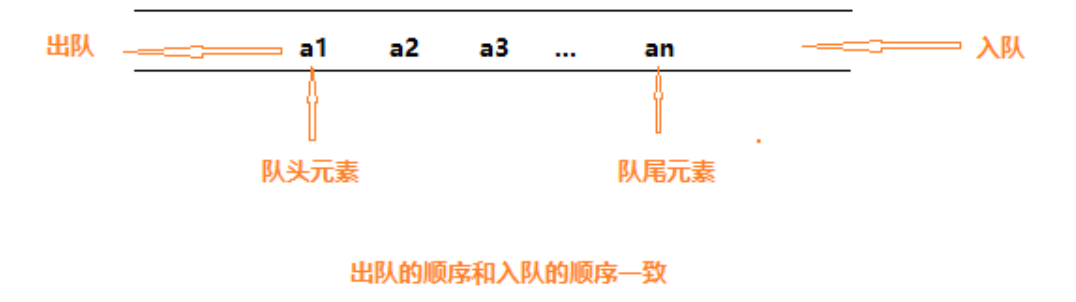
​ 队列是什么？

​ 我们先想一下我们生活中排队的时候的样子。这样一支队伍我们有什么特点。我们队伍最前面的人可以结账离开（出队），最后的人可以随意进入（入队）。中间的人就不可以随意离开（都已经排队了，不想放弃，就这样理解）。

image-20240213001506492image-20240213001541349

一、模拟队列（简单）

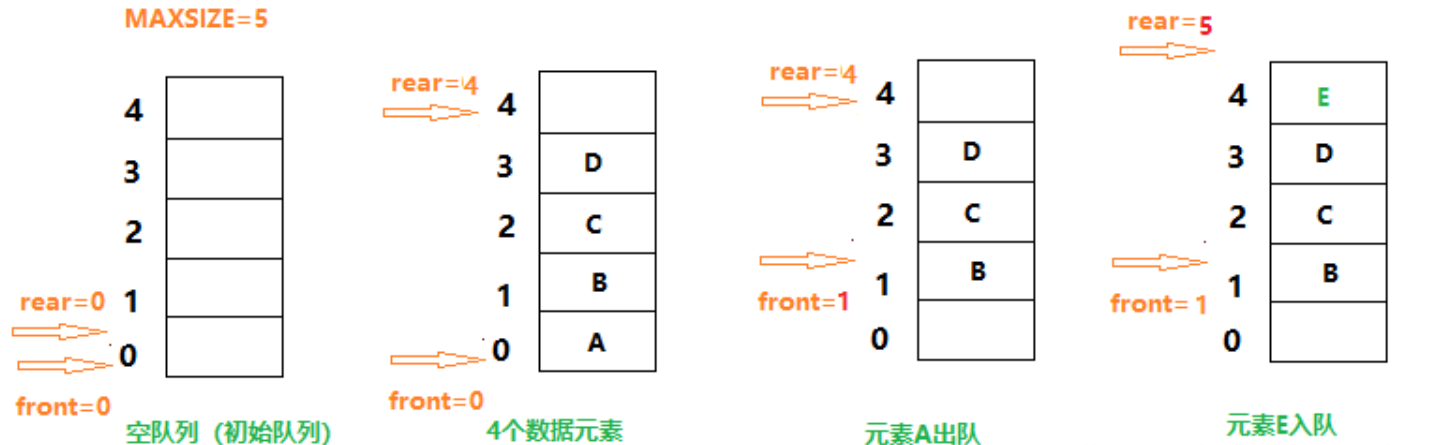
实现一个队列，队列初始为空，支持四种操作：

  1. push x – 向队尾插入一个数 x；
  2. pop – 从队头弹出一个数；
  3. empty – 判断队列是否为空；
  4. query – 查询队头元素。

现在要对队列进行 M 个操作，其中的每个操作 33 和操作 44 都要输出相应的结果。

输入格式

第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围

$$
1≤M≤100000\
1≤x≤10^9
$$

所有操作保证合法。

输入样例：

1
2
3
4
5
6
7
8
9
10
11
10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6

输出样例：

1
2
3
4
NO
6
YES
4

思路

​ 按照队列的基本操作思路走的，基本没什么思路技巧，不懂就直接看代码吧，看不懂问我。

代码

答案（请自己先思考一下再参考） 
        
#include < iostream>
#include < cstdio>
#include < cstring>
using namespace std;
const int N = 1e5 + 10;
int querys[N],top_1,top_2; 
// top_1为队头，top_2为队尾
void push(int x)
{
    querys[top_2++] = x; // 在队尾添加元素
}
void pop()
{
    top_1++; // 队头的人走了后面的跟上，top_1后面的人就是top_1 + 1
}
void empty()
{
    if (top_1 == top_2) printf("YES"); // 想想当一个人都没有的时候，队头和队尾的位置应该是重叠的，反之则不为空
    else printf("NO");
    puts("");
}
void query()
{
    printf("%d\n",querys[top_1]); // 找到队头元素
}
int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        char op[10];
        scanf("%s",op);
        if (!strcmp(op,"push")) 
        {
            int x;
            scanf("%d",&x);
            push(x);
        }
        else if (!strcmp(op,"pop")) pop();
        else if (!strcmp(op,"query")) cout << querys[top_1] <<'\n';
        else 
        {
            if (top_2 == top_1) cout << "YES\n";
            else cout << "NO\n";
        }
    } 
    return 0;
}

二、滑动窗口（中等-）

给定一个大小为 n≤10^6^ 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

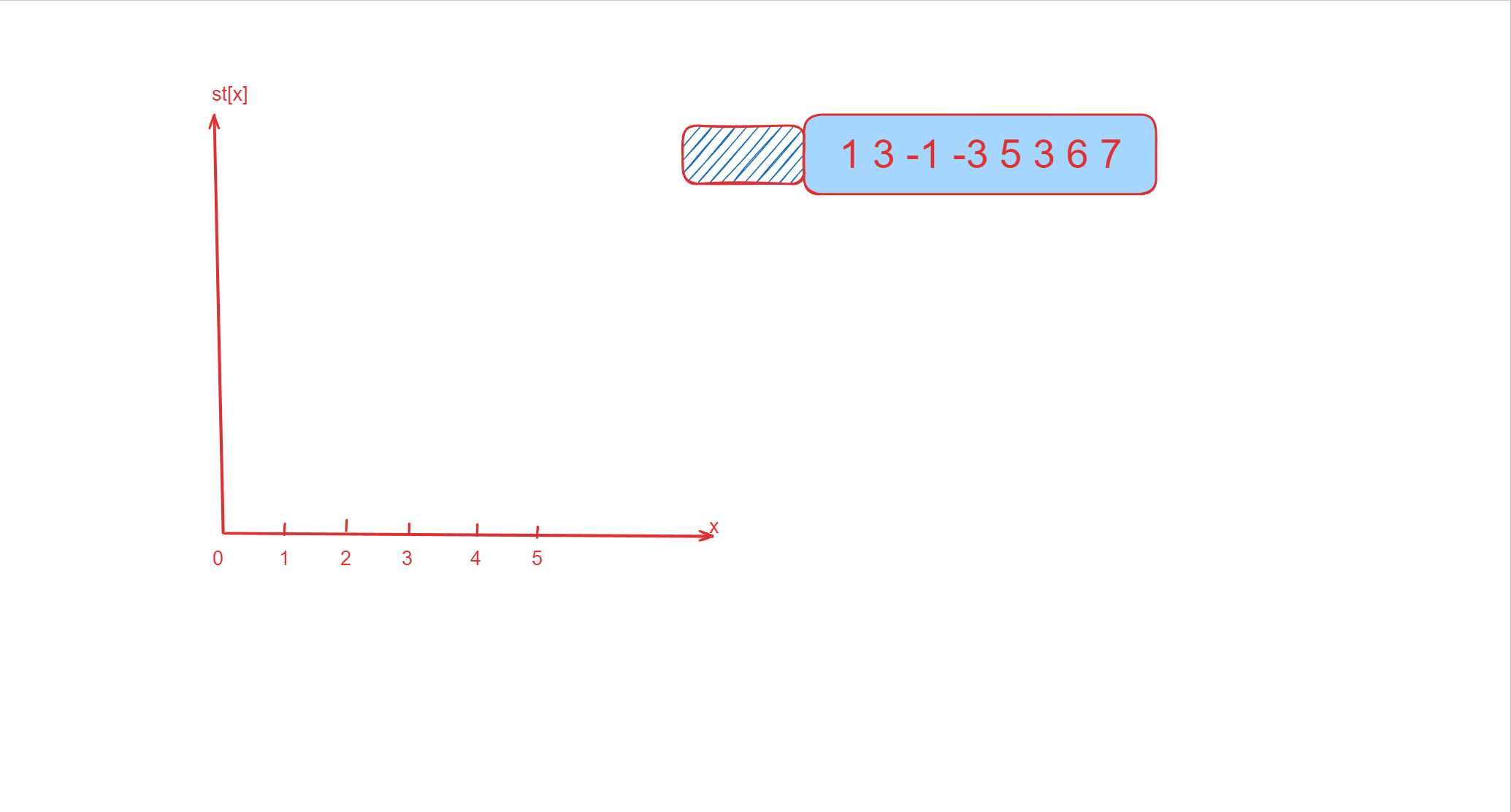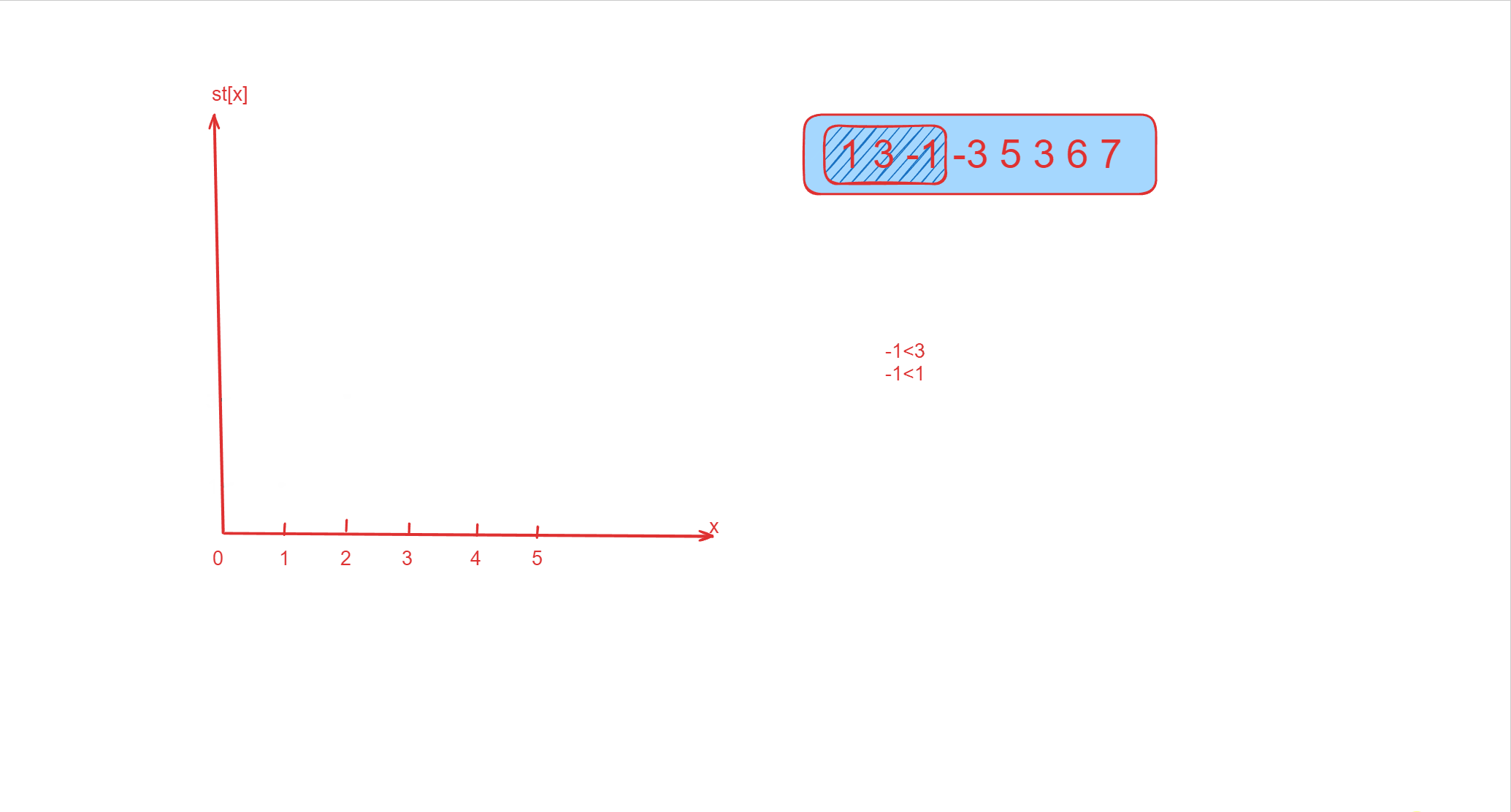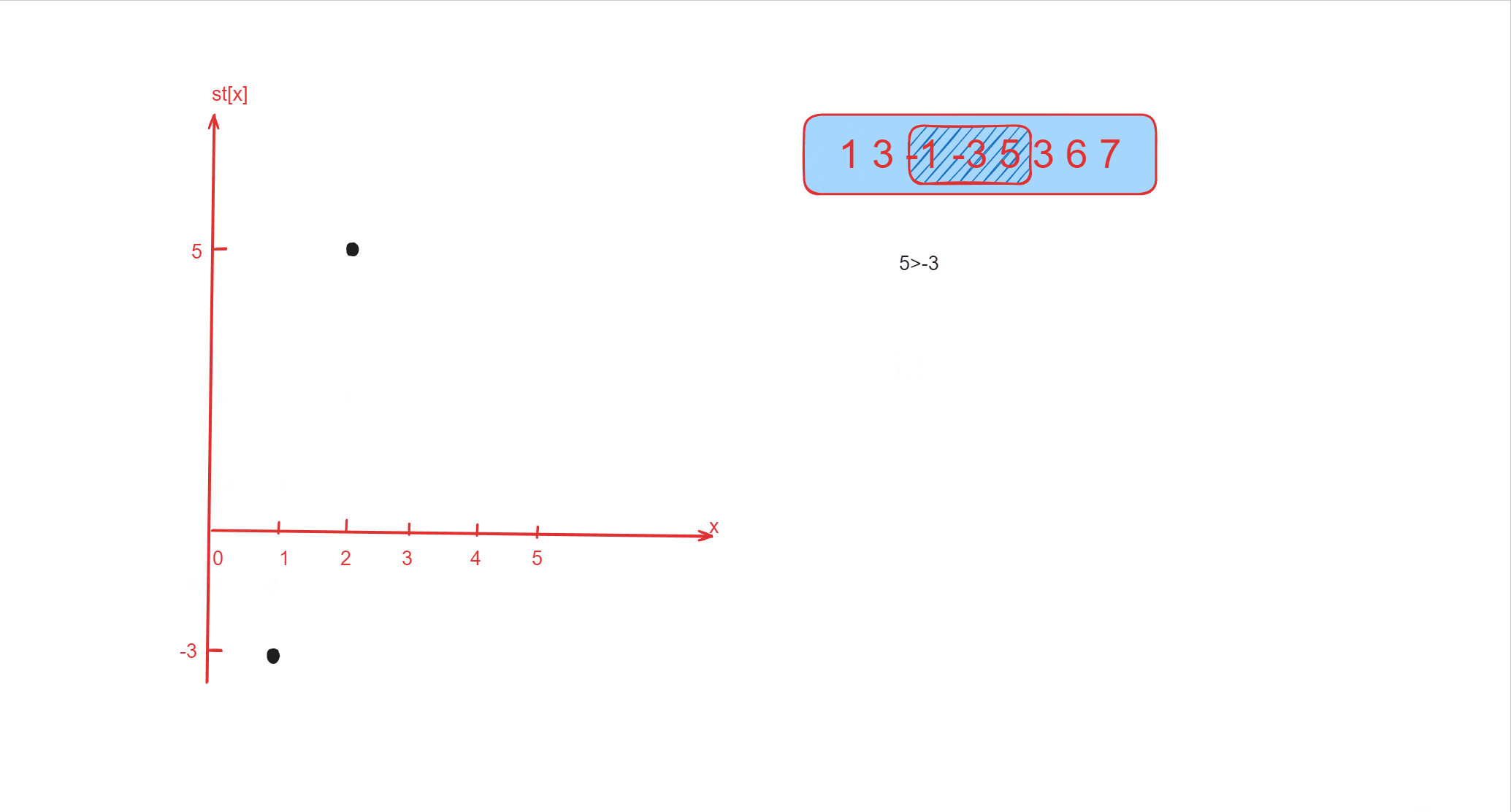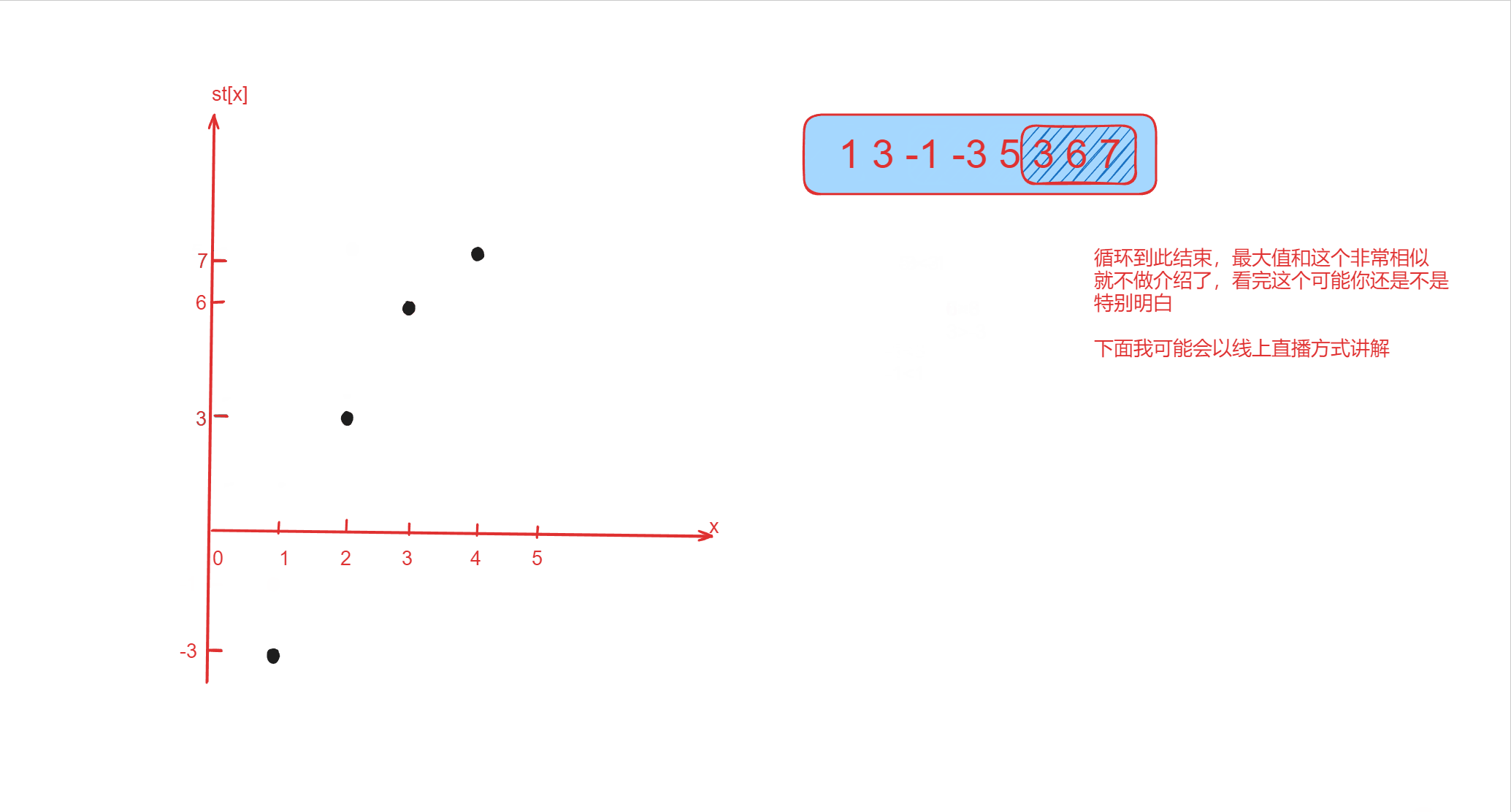
该数组为 [1 3 -1 -3 5 3 6 7]，k 为 33。

窗口位置 最小值 最大值
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

1
2
8 3
1 3 -1 -3 5 3 6 7

输出样例：

1
2
-1 -3 -3 -3 3 3
3 3 5 5 6 7

思路（实在搞不懂就直播录屏，和我提！！！）

动画2

代码

答案（请自己先思考一下再参考） 
        
#include < iostream>
#include < algorithm>
using namespace std;
const int N = 1e6 + 10;
int n, k;
int a[N],q[N];
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin >> n >> k;
    for (int i = 0; i < n; i++) cin >> a[i];
    int hh = 0, tt = -1;
    for (int i = 0; i < n; i++) {
        if (hh <= tt && i - k + 1 > q[hh]) hh++;
        while (hh <= tt && a[i] <= a[q[tt]]) tt--;
        q[++tt] = i;
        if (i - k + 1 >= 0) cout << a[q[hh]] << " ";
    }
    puts("");
    hh = 0,tt = -1;
    int q[N] = {0};    
    for (int i = 0; i < n; i++) {
        if (hh <= tt && i - k + 1 > q[hh]) hh++;
        while (hh <= tt && a[i] >= a[q[tt]]) tt--;
        q[++tt] = i;
        if (i - k + 1 >= 0) cout << a[q[hh]] << " ";
    }
    return 0;
}